안경에 낀 먼지를 닦고 스터디를 하기로 결정!

Written by 백승언 on 25 Feb 2024

안녕하세요, 저는 “안경에 낀 먼지를 닦고 의사결정” 아카데미 스터디를 빌드한 백승언입니다.

이 글에서는, (1) 2024년 상반기에 진행할 본 스터디에 대한 간단한 소개과 (2) 저에 대한 간단한 소개, (3) 스터디 계획을 소개해 드리고, 의사결정을 연구하는 방법론 중 하나인 게임이론을 통해, (4)왜 스터디에 참여해야 하는지를 실제 가짜 연구소 내 스터디 사례를 기반으로 분석한 내용을 공유드리고자 합니다.

“안경에 낀 먼지를 닦고 의사결정” 스터디 소개

해당 스터디에서는, 불확실한 상황에서의 의사결정(MAB, 결정 이론, 최적 제어, 게임이론, … 등)과 관련된 다양한 분야에 초점을 맞추어 공부를 해 보고자 만들어 졌으며, 책 1권과 자유롭게 선택한 논문을 매주 함께 공부해 나가는 것을 목표 하고 있습니다.

*가짜연구소 8기에서 진행되는 프로젝트는 계획표)를 참고해주세요.

빌더 소개

저는 다양한 분야에서 강화학습의 연구 개발을 수행해온 백승언 이라고 합니다.

가짜 연구소에서는 5기 부터 참여한 스터디를 8기까지 쭉 참여하고 있으며(모여봐요 강화의숲), 강화학습 외의 조금 더 다양한 의사결정 분야에서 불확실성이라는 테마를 다루고 싶어 해당 스터디를 spin-off 개념으로 열게 되었습니다.

스터디 계획

스터디의 계획은 다음과 같습니다.

매주 선정한 교재의 진도를 나가며, 쏟아지는 업무 및 논문에 파묻혀 잊어가던 기초를 다시 다지는 시간을 가지고자 합니다.
또한, 다양한 분야에서 불확실성 혹은 의사결정을 어떻게 다루는지에 대해 논문을 기반으로 논의하며, 다양한 자극을 얻을 수 있는 시간을 가지고자 합니다.

본 스터디가 이러한 두 마리 토끼를 잡고자 하는 어려운 계획을 가지고 있지만, 성실하시고 훌륭하신 분들과 함께 헤쳐나가고 싶습니다.

게임 이론으로 분석한 스터디를 해야 하는 이유

본 스터디의 제목은 안경에 낀 먼지를 닦고 의사결정입니다. 이를 풀어서 말하면 다음과 같습니다. 이득이 되는 상황인지 아닌지에 불확실한 상황에서, 어떻게 최선의 의사 결정을 할 것인가?

이는 사실 우리가 매일, 매시간 접하는 문제입니다. 게임을 시작하고 싶은데 어떤 게임을 할까? 어떤 직업을 할까? 등등 사소한 취미 생활에서 마주하는 문제부터, 어떤 회사에 지원할까? 대학원에서는 어떤 전공을 할까?와 같은 중차대한 문제들까지도 모두 이러한 의사결정 렌즈를 통해 우리는 선택을 해야 합니다.

이는, 이 글을 읽고 계신 여러분의, "내가 이 스터디를 하는게 좋을까? 혹은 가짜연구소 활동을 하는게 좋을까?"의 고민 역시 마찬가지라고 생각합니다.

그리하여, 이 밑 부터는 스터디 커뮤니티 활동을 해야하는 이유에 대해 게임이론 렌즈를 빌려와 분석해 보았습니다. 제가 게임이론 전문가가 아니니 재미로 읽어주세요! :)

이 글을 읽고 계신 여러분! 우리는 왜 스터디 커뮤니티 활동을 해야 할까요? 하면 정말 좋을까요? 이에 대한 긍정적인 의견 혹은 부정적인 의견이 다양 하겠지만, 저는 이득(payoff) 관점에서만 이를 분석했다는 것을 말씀 드리며 포스팅을 시작하겠습니다.

먼저, 목차는 다음과 같습니다.

도입부에서는, 이런 글을 제가 써도 괜찮을지에 대한 정당성을 조금 확보하기 위해, 제가 스터디 커뮤니티 활동을 다양하게 했다는 증빙? 과정을 마친 후, 역사적으로 존재했던 스터디 커뮤니티 두 곳에 대해 간단히 설명 드리고자 합니다.

그 다음 본 내용에서는, 스터디 커뮤니티 활동을 하는것이 이득이 되는지에 대해 게임이론 적으로 분석하는 내용을 준비해 두었으며, 구체적으로는 (1) 게임이론의 기본 모델 중 죄수의 딜레마(Prisoner’s Dilemma), 사슴사냥(Stag Hunt) 게임에 대한 소개와 (2) 이타적 전략의 생존 조건을 분석하기 위해 제안된 볏짚 모형(Haystack model)과 이 모형을 이용한 스터디 활동에 대한 분석을, (3) 마지막으로 이렇게 분석된 내용을 가짜 연구소 내 실제 스터디 사례들과 엮어서 분석 결과에 대한 정당성을 조금 챙겨보고자 합니다.

그 후, 결론을 통해 포스팅을 마무리 하겠습니다.

먼저, 도입부입니다.

본 발표에 앞서, 저에 대해 간단히 소개해 드리자면, 저는 강화학습을 좋아하고, 강화학습 관련된 얘기를 다른 사람들과 함께 나누는 것을 좋아하는 사람입니다.

그렇기에, 많은 곳들에서 강화학습과 관련된 얘기들을 나누기 위해, 정말 다양한 커뮤니티들에 참여해 왔습니다. 강화학습이 주 토픽인 팀블로그 뿐만 아니라, 학계 분들이 계시는 Papers with Code, 업계/학계의 분들이 논문을 함께 읽는 강화학습 논문 리뷰 스터디, 가짜 연구소, 딥러닝 논문 읽기 모임 등등….

저는 이러한 활동들을 통해서 얻은 것들이 정말 너무 많았기에, 이번 스터디 홍보글을 통해 왜, 스터디를 해야 하는지를 정말 너무나도 말하고 싶었고, 그리하여 해당 포스팅을 준비 했던 것 같습니다.

또한, 강화학습이라고 하는, 의사결정과 관련된 분야에서 연구개발 업무를 수행하는 이과(not T)이기에, 스터디를 해야하는 이유를 정량적으로 혹은 수학적으로 설득 하고자 하는 것도 해당 포스팅을 하게 된 이유라고 말씀드리고 싶습니다.

포스팅을 위해 조사를 해 보니, 사실 스터디 커뮤니티 활동이라는 것은 인터넷 기술이 발달한 오늘날의 얘기만은 아니라는 것을 알 수 있었습니다.

기원전에도, 유명한 철학자인 탈레스, 그리고 그와 유사한 생각을 가지던 철학자들은 새로운 철학, 과학을 공부하기 위해 모였으며, 그들을 이오니아 학파 혹은 밀레스토 학파로 칭하며, 다양한 만물의 근원에 대해 연구 및 커뮤니티 활동을 해왔다고 합니다.

조금 더 현대로 가까이 오면, 누구나 알고 있는 유명한 과학자인 아인슈타인의 경우에도, 물리학, 과학 철학 등에 대한 얘기들을 나누는 올림피아드 아카데미라고 하는 커뮤니티 활동을 했다고 합니다.

이렇듯, 스터디 커뮤니티 활동은 자연스럽게 진화하여 현재까지 살아남은 하나의 문화이며, 공부한 내용에 대해 의견을 나누며 그 깊이를 쌓아가고자 하는 것은 천재라고 불리우는 뛰어난 사람들에게도, 일반적인 활동이라는 것을 알 수 있었습니다.

그럼에도 불구하고, 저는 조금 더 수학적으로 혹은 정량적으로 이러한 스터디 활동을 하는 이유에 대해서 분석을 해보고 싶었습니다.

그리하여, 본 슬라이드 부터는 게임이론 관점으로 스터디 커뮤니티 활동을 분석한 내용을 공유드리겠습니다.

먼저, 게임이론에서 연구되는 기본 모형인 죄수의 딜레마와, 사슴사냥 문제에 대해서 소개 드리겠습니다.

이 두 게임 모두, two-player가 존재하는 상황에서, 게임의 결과로 얻는 두 명의 플레이어들의 보수(payoff)의 합이 0보다 큰, 협력 게임이라는 것을 말씀 드립니다. 이와 반대되는 게임으로는 바둑, 체스와 같은 경쟁 게임이 존재합니다. (two-player zero-sum game)

먼저, 죄수의 딜레마의 경우, 1950년 두 분의 교수님들에 의해 제안된 게임으로, 두 죄수 모두 협력을 하여 서로의 죄목에 대해 침묵하면 두 죄수 모두 적은 형량을, 둘 중 한 명이라도 배신을 하면 배신 당한 죄수는 큰 형량을, 둘 다 배신을 하면 둘다 적절히 큰 형량을 살게 될 때, 죄수들의 행동에 대해 연구를 하고자 만들어진 모델입니다.

이와 조금은 다른 사슴사냥의 경우, 저명한 장자크 루소의 저서에서 영향을 받아 제안된 모델이라고 하며, 두 사냥 꾼 모두 협력하여 사슴을 잡으면 며칠을 굶지 않아도 될 고기를 얻고, 둘 중 한명은 토끼를 잡을 경우 사슴 사냥에 나선 사냥꾼은 허탕을, 나머지 사냥꾼은 하루 이틀 때울 고기를 얻게 되고, 마지막으로 두 사냥 꾼 모두 토끼를 사냥하면 모두 하루 이틀 때울 고기만 얻게 되는 게임으로써, 이 모델 또한 협력 행위를 연구하고자 만들어진 모델입니다.

저는 이 중, 스터디 커뮤니티 활동을 사슴사냥 문제로 모델링 하고자 하였습니다. 자세한 사항은 이어서 설명 드리겠습니다.

먼저, 스터디 활동 자체를 고민하고 계신 분들이 가지고 계시는 문제를 분석하기 위해 스터디 그룹 참가(SGP) 모델, 그리고 스터디 활동에서 남들이 열심히 안 하면 어떡하지..를 걱정하고 계신 분들의 문제를 분석하기 위해 스터디 그룹 내 공부(SSG) 모델을 모델링 하였습니다.

그 전에, 가정으로써 이 게임에 참가하는 모든 구성원들은 동일한 능력을 가지며, 동일하게 성실하다는 가정을 하였습니다. 또한, player는 단순하게 2명으로 고정하였습니다.

그리하여, 사슴사냥 문제로 모형화한 SGP 모델에서는, 함께 협력적으로 준비하여 공부를 할 경우 얻는 이득을 K로, 혹은 혼자 공부함으로써 얻는 이득을 3으로 두었습니다.

그리하여, 이 경우에는 정말 단순하게 함께 공부하면서 얻는 이득인 K가 3보다 큰 경우, 스터디에 참여하는게 다른 조건 없이 이득인! 전략임을 알 수 있었습니다.

정말 나쁘게 말하면 참여하고, 그 시간에 나 혼자 공부를 해도 최소 3의 이득을 얻으니까요. (찬란님, 가짜연구소 관계자 분들, 저는 그렇게 살아오지 않았습니다…ㅎ)

그렇다면, 스터디 그룹 내에서의 스터디원들의 전략에 따른 보수 행렬(Payoff matrix)과, 최적의 전략은 어떤 것인지, SSG 모델에 대한 분석을 시작하겠습니다.

먼저, 해당 모델을 분석함에 앞서서, 몇 가지 가정을 추가하도록 하겠습니다.

스터디 활동은 다음과 같은 과정으로 진행됩니다: 혼자 공부하는 과정, 자료 준비 과정, 토론 과정.

자료 준비를 하는 과정은 혼자 공부하는 시간을 뺏음으로써, 혼자 공부함에 따라 얻는 이득을 1 깎는 다는 가정을 두었으며, 또한 다른 플레이어는 해당 자료를 통해 1의 이득을 얻는다고 가정하였습니다.

토론 과정 동안, 두 플레이어는 2의 이득을 얻는다고 가정하였습니다. (토론을 통한 이득은 한 명이라도 준비를 해오지 않을 경우 발생하지 않습니다.)

해당 가정들을 통해, 스터디 그룹 내에서 공부하기 모델(SSG)모델의 보수 행렬은 다음과 같이 설계되었습니다.

모든 플레이어가 협력 할 경우, 두 플레이어는 9점을 받습니다. (혼자 공부2 + 동료가 공부한 내용3, 나와 동료의 자료2, 토론2)

모든 플레이어가 기만 행위를 할 경우, 두 플레이어는 자신의 공부를 수행했다는 가정이 있으므로, 모두 3점을 받습니다.

한 플레이어는 협력을, 다른 플레이어는 기만 행위를 할 경우, 협력적인 플레이어는 3점(혼자 공부2 + 나의 자료 1)을, 기만행위를 한 플레이어는 7점을(혼자 공부3 + 동료가 공부한 내용 3 + 동료의 자료 1) 받습니다.

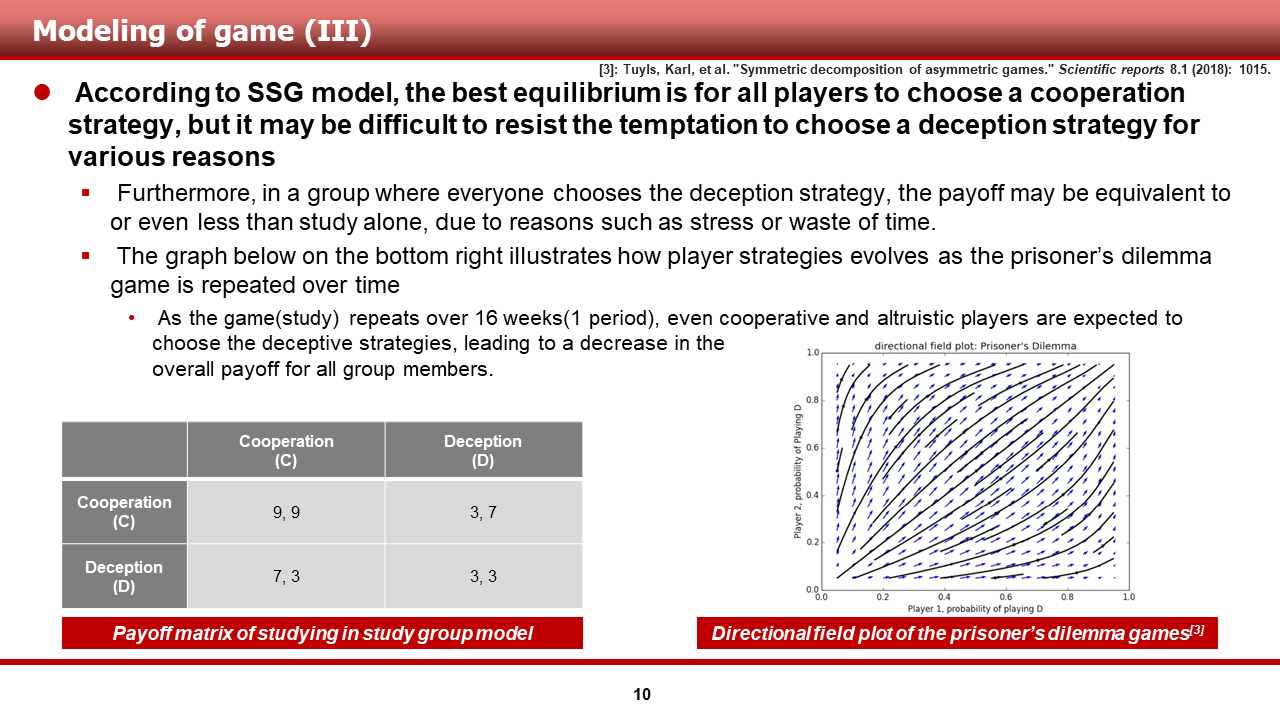
이렇게 설계된 SSG 모델에 따르면, best equilibrium은 물론 두 플레이어 모두 협력을 수행하는 것이라는 것을 쉽게 알 수 있습니다. 하지만, 보수 행렬을 보면 알 수 있다 싶이, 사람이라면 기만 행위에 대한 욕심을 버리기가 쉽지 않은 것을 알 수 있습니다. (너무 피곤하다던가, 다른 약속 등이 앞서는 등의 다양한 이유로)

그렇지만, 이렇게 그룹 내 모든 멤버들이 기만 전략을 선택할 경우, 스터디 그룹을 함께하는 것의 의미는 퇴색됩니다. 모두가 기만 번략을 선택한다면, 굳이 시간을 내서 모이지 않더라도, 혼자 공부했을 때 얻는 이득이 3점이기 때문입니다.

이는 죄수의 딜레마 게임이 반복된다는 가정 하에서, 플레이어 들의 전략의 변화가 D로 변한다는, 오른쪽 밑의 그림을 통해서도 쉽게 알 수 있습니다. 기만 전략 혹은 배신 전략을 한 명이라도 선택 하기 시작하면, 다른 플레이어는 바보가 아닌 이상 협력을 멈추게 되는 것입니다.

이는 슬픈 분석 결과입니다. 여러 명이 모인 스터디 그룹의 특성상, 발생하기 쉬운 상황(누군 가의 기만 전략 선택)이 결국 그룹을 파멸로 이끌 수 있다는 것을 보여주니까요.

그런데, 정말 그럴까요? 저희는 알고 있습니다. 고대 스터디 커뮤니티인 탈레스의 이오니아 학파의 연구 결과는, 신이 전부였던 세상의 근간을 흔들어서 결국 현대의 양자역학까지 다다르게 되었으며, 아인슈타인의 올림피아드 아카데미 활동은 몇년 후, 그가 시간과 공간에 대한 기본 개념을 바꿔버린 상대성이론 탄생의 밑거름이었다는 것을요.

그게 어떻게 가능한 일일까요? 죄수의 딜레마 모형은 이를 설명할 수 없는데 말입니다.

그리하여, 저는 스터디 그룹 내에서 함께 공부하는 것이 스터디 참여자들에게 이점을 가져와 줄 수 있다는 결론을 내어, 고민하시는 분들께 힘을 실어드리겠습니다!

이를 위해, 이 장에서는 이를 설명 할 수 있는 다른 모형(볏짚 모형)을 빌려와 분석을 계속 진행해보고자 합니다.

볏짚 모형(Haystack modle)은 존 메이나드 스미스가 1964년 제안한 모델로써, 특정 모집단 내에서 이타적인 전략을 지닌 집단이 살아남는 조건을 연구하기 위해 만들어진 모형입니다.

이 모형은, 추수 후 수확된 볏짚에 살고 있는 이타적인 성향의 쥐들과 이기적인 성향의 쥐들의 번식을 통해 이타적인 성향을 가진 쥐들이 어떻게 살아 남는지를 설명 했기에 이름이 볏짚 모형으로 지어졌습니다.

구체적인 설명은 다음 슬라이드에서 이어 나가겠습니다.

먼저, 이 모델은 다음과 같은 가정들을 필요로 합니다:

각 볏짚은 두 마리의 쥐를 수용할 수 있으며, 쥐들은 각각 이타적인 성향(C), 이기적인 성향(D)을 지니고 있다고 가정합니다

쥐들은 정해진 볏짚을 떠나지 않으며, 한 세대 동안 번식을 수행하고 다음 세대가 태어나면 죽는다고 가정합니다.

이러한 가정을 통해, 메이나드 스미스는 다음과 같은 보수 행렬을 설계 했습니다.

이타적인 쥐들이 한 볏짚에 모일 경우, 자원을 잘 활용하여 q 마리의 이타적인 쥐들을 낳을 수 있습니다.

이기적인 쥐와 이타적인 쥐가 만나면 이타적인 쥐는 자식을 낳을 수 없으며, 이기적인 쥐만 2마리의 이기적인 성향을 지닌 자식을 낳습니다.

이기적인 쥐들이 만날 경우, 자기 몫의 자원을 잘 확보하여, 각자 1마리 씩 총 2마리의 이기적인 쥐를 낳습니다.

이렇게 설계된 보수 행렬은 q가 2보다 클 때는 사슴 사냥 모형과 같으며, q가 1과 2사이일 경우, 죄수의 딜레마 모형과 같다고 합니다.

저는 SSG 모델을 사슴 사냥 게임으로 모델링 하였기에(아무리 그래도 스터디원들이 죄수는 아니죠..!! 사냥꾼도 아니지만… 흠흠..), q가 2보다 크다고 가정하고 분석을 진행 해보겠습니다.

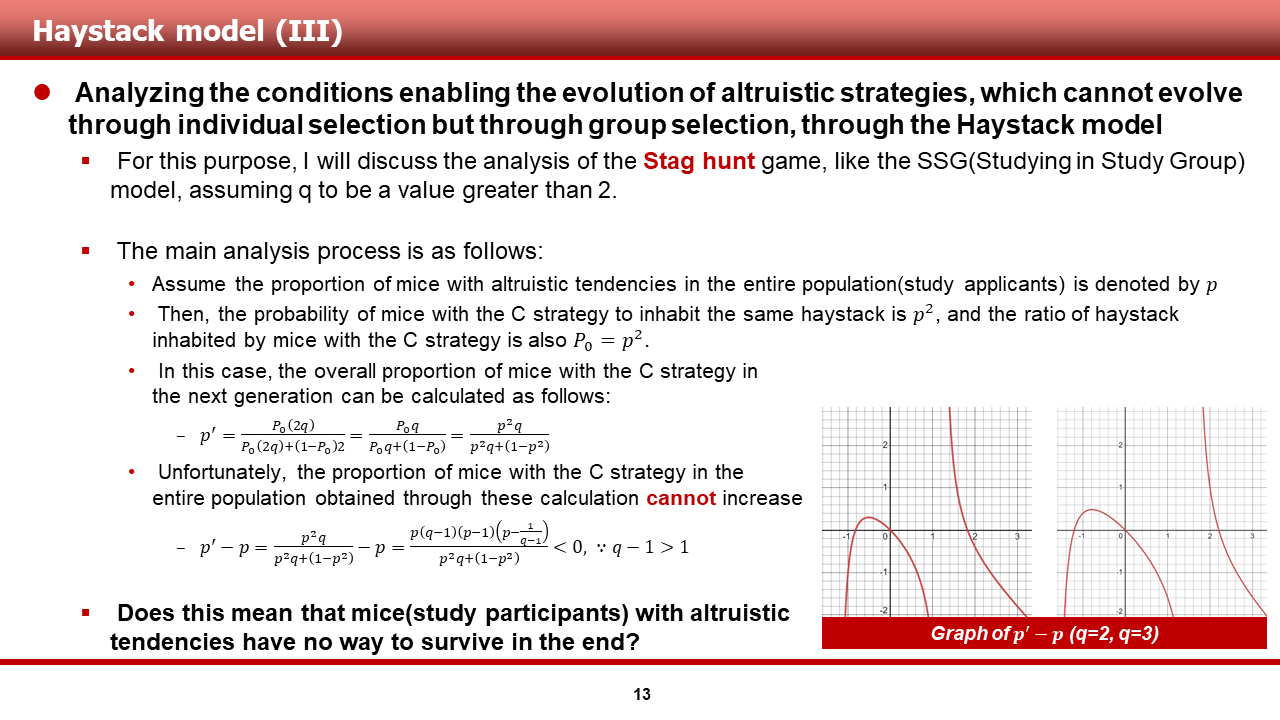
주된 분석 과정은 다음과 같습니다. 전체 모집단 중 이타적인 성향을 지닌 쥐(협력적인 전략을 택하는 스티디 원)들의 비율을 p라고 가정하겠습니다.

이럴 경우, 특정 볏짚에서 이타적인 성향을 가지는 쥐들이 만나는 비율은 p^2임을 알 수 있습니다.

그러면, 우리가 확인하고 싶은 것은 게임이 반복됨에 따라, 이타적인 성향을 지닌 쥐들이 비율이 모집단 내에서 증가하는 것입니다.

이를 위해, 한 세대가 지남에 따른 모집단 내 이타적인 성향을 지닌 쥐들의 비율인 p’과 이전 세대 모집단 내 이타적인 성향을 지닌 쥐들의 비율인 p의 차이인 p’-p가 0보다 크다는 것을 확인하면 됩니다.

결론은, q>2인 사슴사냥 게임에선 그런 일이 일어날 수 없습니다.

이게 무슨 일인가요… 스터디를 정녕 하면 안 되는 것인가요? 저는 다른 사람들과 함께 공부하고 나누며 기쁨을 나누고 싶단 말입니다!

걱정 마십시오! 존 메이나드 스미스맨이 있다구~ 존 메이나드 스미스는 이타적인 성향을 지닌 쥐의 비율이 늘어날 수 있는 조건들을 수학적으로 구하여, 다음과 같이 제시하고 있습니다.

각 그룹은 매우 작은 조상 쥐들로 시작해야 한다.

a) 이는, 이타적인 성향을 지니는 쥐들이 비율이 p로 고정되어 있더라도, 그들 끼리 모인 볏짚이 형성될 확률인 p^n이 n이 높아질수록 기하급수적으로 작아지기 때문에 만들어진 조건입니다. b) 이는 또한, 자기소개서 등으로 이타적인 스터디 참여자들의 비율을 높일 경우 스터디 활동이 원활히 진행되리라는 것을 암시합니다.

하나의 볏짚에 있는 자원은 그들에게만 돌아가야 합니다.

a) 이타적인 성향을 지닌 쥐들은 이기적인 성향을 지닌 쥐들에게 자원을 뺏기는 것에 조금 더 포용적일 것이기 때문입니다. b) 이는, 수료증 등의 스터디 증빙 자료 혹은 다른 benefit들을 정식으로 참여한 스터디 원들에게만 수여해야 한다는 것을 의미할 수 있습니다.

각 볏짚 내 쥐들은 볏짚 내에서 여러 주기(t 주기) 동안 번식을 해야 합니다.

a) 이럴 경우, p’를 계산하는 식에서 q가 q^t로 변모하여, 모집단 내 이타적인 성향을 지닌 쥐들의 비율을 늘리기 때문입니다. b) 이는, 스터디 커뮤니티 차원에서 여러 주기 동안 진행되는 스터디 그룹의 활동을 권장하는 것이 긍정적이라는 것을 암시할 수 있습니다.

과거를 돌아보면, 다행히도 제가 참여했던 혹은 참여중인 팀 블로그, 스터디 그룹, 가짜 연구소 등은 이런 조건들을 만족 했던 것 같고, 만족하지 않더라도 초기 비율 p가 높았던 것 같습니다. :D

이번 장은, 도출된 결론을 통해 협력적인 성향을 가지신 잠재적 스터디원 분께서 가짜 연구소 활동에 지원 하는 것을 응원 하고자 만들었습니다.

구체적으로는, 볏짚 모형에서 말하는 이타적 성향을 지닌 쥐들이 살아남을 조건을, 가짜 연구소는 어떻게 만족하는지에 대한 분석을 준비했습니다.

각 그룹은 적은 수의 시조로 구성되어야 한다.

a) 해당 조건은 정확히는 모집단에서 이타적인 쥐들로만 모인 볏짚이 생성될 확률인, p^n이 작아지는 것을 방지하기 위한 조건입니다. 이를 위해, 가짜 연구소는 자기소개서와 다른 스터디에 참여한 이력 등을 보며, n을 작게하는 접근 보다는 p를 높이는 접근을 선택 했습니다. b) 또한, 볏짚 모형과 달리, 가짜 연구소는 다양한 제도(규제)를 통해서, 협력적이지 않은 스터디원들에게 수료증을 주지 않는 등의 penalty를 주고 있습니다. 이는 payoff matrix를 협력적인 스터디원들에게 유리하게 수정하는 것을 의미하며, 이를 통해 협력적인 행위를 했을때 얻는 이득이 커질 수 있습니다. c) 마지막으로, 볏짚에 임의로 할당 되는 볏짚 모형의 쥐들과 달리, 가짜 연구소는 관심 있는 스터디에 직접 지원을 하는 지원제도를 사용하고 있습니다. 이는 개인의 평판 등을 이유로 기만적인 행위를 했을때의 payoff에 penalty를 받는다는 것이며, 또한 모두가 협력적인 행위를 했을 때의 payoff가 더욱 크다는 것을 의미하므로, 협력적인 전략을 선택하는 것이 유리한 게임임을 의미합니다.

하나의 볏짚에 있는 자원은 그들에게만 돌아가야 합니다.

a) 가짜 연구소의 스터디 수료증은 정식으로 참여한(볏짚 내의) 스터디 지원자들에게만 주어집니다. 또한, 청강 제도를 유지하고 있기에 자원이 공유되는 것이 아니냐고 생각할 수 있지만, 경험상 이는 다른 협력적인 전략을 가진 스터디원을 보충할 수 있는 제도로 활용되는 것이 일반적이었습니다. 즉, p를 높이는 제도입니다.

각 볏짚 내 쥐들은 볏짚 내에서 여러 주기(t 주기) 동안 번식을 해야 합니다.

a) 가짜 연구소는 수행 됬던 아카데믹 프로그램의 “다회차” 빌딩을 격려하는 커뮤니티입니다. 이에 따라, 협력적인 스터디원들로만 모인 스터디 그룹은 여러 회차를 반복하게 되며, 이에 따른 산출물들의 양과 질은 스터디 그룹이라고는 믿을 수 없을 만큼 높다는 것을 알 수 있습니다.

이어지는 슬라이드에서는 “다회차” 스터디 그룹에 조금 더 집중하여, 분석 결과에 대한 정당성 확보와 지원자들의 의사결정을 응원하는 내용을 공유드리겠습니다.

첫 번째 사례는 가짜 연구소 내 Causal Inference Research Group입니다. 가짜 연구소는 아카데믹 프로그램을 다회차 유지할 경우 Research Group으로 승격, 더욱 다양한 지원을 아끼지 않는데요, 그 중 하나가 인과추론 스터디 그룹이라고 봐주시면 될 것 같습니다.

해당 그룹은 초기(4기)부터 시작하여 8기까지 스터디가 이어지고 있으며, 볏짚 모형의 예측 결과 처럼, 정말 많은 산출물들과 개인의 성장을 보이고 있습니다

그리하여, 최근에는 오픈 소스와 함께 책과 논문까지도 출판 했다는 것은 놀라울 따름입니다.

두 번째 사례는 가짜 연구소 내 Meta-RL Research Group입니다. 이 또한 아카데믹 스터디 그룹에서 시작하여 Research Group으로 이번 8기에 승격된 그룹입니다.

해당 그룹 또한 5기 부터 시작하여 8기까지 스터디가 이어지고 있으며, 이 그룹 역시 볏짚 모형의 예측대로, git book 등의 다양한 산출물들과 개인의 성장을 보이고 있습니다.

또한, 해당 리서치 그룹 내 두 명의 빌더를 양성 했으며, 추후 다양한 project, 책 및 논문 출판등을 계획하고 있습니다.

또한, 혼틈 광고를 수행하자면, 앞서 소개드린 Meta-RL Research group에서 spin-off격으로 새로 빌드된 아카데믹 스터디 그룹이 두 개 있습니다.

하나는 제가 빌드한 안경에 낀 먼지를 닦고 의사 결정이며, 하나는 이홍규님이 빌드해주신 Offline RL로 구현하는 만화경 사륜안입니다.

모두 그 근간은 RL에 있지만, 프로젝트 사이드(Offline RL …), 익스텐션 사이드(안경에 낀 …)로 나온 spin-off라고 이해해 주시면 감사할 것 같고, 9기 때도 꼭 저나 홍규님이 아니어도 Meta-RL 그룹에서 이런 spin-off study들이 나온다면 관심을 가져 주시면 감사할 것 같습니다.

결론입니다.

스터디 커뮤니티에 참가하는 것은 연구, 업무로 바쁜 현대인에게는 정말 힘든 일입니다. 또한, 모델 분석을 통해 free rider가 존재할 경우, 이점이 불확실 하거나 낮을 수 있다는 것은 사실입니다.

하지만 볏짚 모형을 통한 분석 결과는, 특정 조건들을 만족하는 경우에 협력적이지 않은 전략을 선택한 참여자들의 long-term benefit은 결국 적어진 다는 것을 확인할 수 있었습니다. (이타적인 당신은 틀리지 않았습니다!)

뿐만 아니라, 가짜 연구소 내 오래 지속된, 이러한 이타적인 참여자들이 많은 스터디 그룹들은 뛰어난 산출물들을 내고 있음을 case study를 통해 확인할 수 있었습니다.

이를 Casual Inference 스터디 그룹, Meta-RL 스터디 그룹 등의 실제 사례를 통해 증빙하였습니다.
가짜 연구소 내에는, 이 두 스터디 그룹 말고도 더 많은 오래 지속되며 산출물들을 많이 내는 스터디 그룹들이 있으며, 글의 길이가 너무 길어지는 바람에 생략 되어서 아쉬울 정도입니다.

그리하여, 저는 이 글을 통해 장기적 안목을 가지고, 스터디 커뮤니티에 참여하셔서 협력적인 전략을 선택하는 것은 옳은 의사결정임을 주장합니다.